前言

这篇文章总结了二叉树常见的操作集合，大体从递归非递归给出代码实现，包括以下各个操作：

  • 遍历二叉树
  • 建立二叉树
  • 插入节点
  • 查找节点
  • 删除节点
  • 求树的高度

遍历二叉树

递归遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public void rPreOrderTraversal(Node<T> root) {
    if (root != null) {
        System.out.print(root.getData()+" ");
        rPreOrderTraversal(root.getLeft());
        rPreOrderTraversal(root.getRight());
    }
}

public void rInOrderTraversal(Node<T> tree) {
    if (root != null) {
        rPreOrderTraversal(root.getLeft());
        System.out.print(root.getData()+" ");
        rPreOrderTraversal(root.getRight());
    }
}

public void rPostOrderTraversal(Node<T> tree) {
    if (root != null) {
        rPreOrderTraversal(root.getLeft());
        rPreOrderTraversal(root.getRight());
        System.out.print(root.getData()+" ");
    }
}

非递归遍历

非递归遍历借助堆栈实现
前序与中序：

  1. 遇到一个节点，压栈，并遍历其左子树
  2. 左子树遍历结束后，栈顶弹出节点
  3. 对弹出节点的右子树进行先（中）序遍历

区别 => 访问时刻：入栈时访问节点是先序，出栈时访问节点为后续

后序：
采用两个栈，栈1保存遍历顺序，栈2保存访问的倒序。
下图是前序、中序、后序的访问顺序：

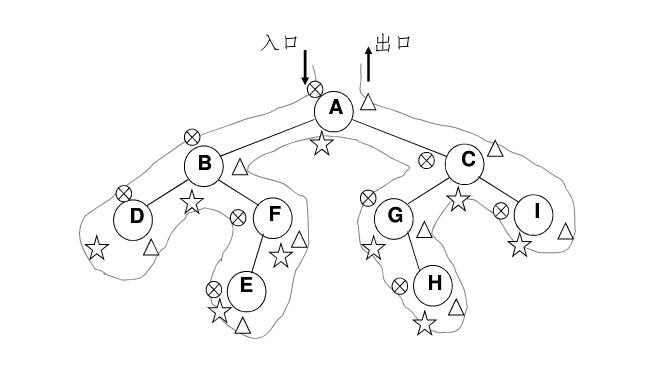
注：电灯泡符号、三角形、星号分别表示前序、中序、后序访问各节点的时刻

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
public void preOrderTraversal(Node<T> root) {
    Stack<Node<T>> stack = new Stack<Node<T>>();
    Node<T> tree = root;

    while (tree != null || !stack.empty()) {
        while (tree != null) {
            System.out.print(tree.getData()+" ");
            stack.push(tree);
            tree = tree.getLeft();
        }

        if (!stack.empty()) {
            tree = stack.pop();
            tree = tree.getRight();
        }
    }
}

public void inOrderTraversal(Node<T> root) {
    Stack<Node<T>> stack = new Stack<Node<T>>();
    Node<T> tree = root;

    while (tree != null || !stack.empty()) {
        while (tree != null) {
            stack.push(tree);
            tree = tree.getLeft();
        }

        if (!stack.empty()) {
            tree = stack.pop();
            System.out.print(tree.getData()+" ");
            tree = tree.getRight();
        }
    }
}

public void postOrderTraversal(Node<T> root) {
    Stack<Node<T>> s1 = new Stack<Node<T>>();
    Stack<Node<T>> s2 = new Stack<Node<T>>();

    if (root != null) { // 先将根节点入栈
        s1.push(root);
    }
    Node<T> tempNode;
    while (!s1.empty()) {
        tempNode = s1.pop(); // 弹出当前根节点
        s2.push(tempNode); // 当前根节点入栈
        // 根节点的左右子节点入栈
        if (tempNode.getLeft() != null) { 
            s1.push(tempNode.getLeft());
        }
        if (tempNode.getRight() != null) {
            s1.push(tempNode.getRight());
        }
    }

    while (!s2.empty()) {
        System.out.print(s2.pop().getData()+" ");
    }
}

层序遍历

借助队列先进先出性质实现层序遍历

  1. 将根节点入队
  2. 执行循环：节点出队，访问该节点，左右儿子入队
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public void levelOrderTraversal(Node<T> root) {
    if (root == null) {
        return;
    }
    Queue<Node<T>> queue = new LinkedList<>();
    queue.offer(root);
    while (!queue.isEmpty()) {
        Node<T> temp = queue.poll();
        System.out.print(temp.getData() +" ");
        if (temp.getLeft() != null) {
            queue.offer(temp.getLeft());
        }
        if (temp.getRight() != null) {
            queue.offer(temp.getRight());
        }
    }
}

建树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
public Node<Integer> create(){
    InputStream is = null;
    Node<Integer> tree = null;
    try {
        is = new BufferedInputStream(new FileInputStream(new File("BinTree.txt")));
    } catch (Exception e) {
        e.printStackTrace();
    }
    System.setIn(is);
    Scanner sc = new Scanner(System.in);
    tree = buildTree(tree, sc);
    return tree;
}

public Node<Integer> buildTree(Node<Integer> root, Scanner sc) {
    if (!sc.hasNext()) {
        return null;
    }

    Integer data = sc.nextInt();
    if (data == -1) {
        return null;
    } else {
        root = new Node<>(data);
        root.setLeft(buildTree(root.getLeft(), sc));
        root.setRight(buildTree(root.getRight(), sc));
    }

    return root;
}

插入节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public Node<Integer> insert(Integer t, Node<Integer> root) {
    if (root == null) {
        root = new Node<>(t);
        root.setLeft(null);
        root.setRight(null);
    } else {
        if (t < root.getData()) {
            root.setLeft(insert(t, root.getLeft()));
        } else if (t > root.getData()) {
            root.setRight(insert(t, root.getRight()));
        }
    }
    return root;
}

查找节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
public Node<Integer> find(Integer t, Node<Integer> root) {
    if (root == null) {
        return null;
    } else if (t > root.getData()) {
        return find(t, root.getRight());
    } else if (t < root.getData()) {
        return find(t, root.getLeft());
    } else {
        return root;
    }
}

public Node<Integer> iterFind(Integer t, Node<Integer> root) {
    while (root != null) {
        if (t > root.getData()) {
            root = root.getRight();
        } else if (t < root.getData()) {
            root = root.getLeft();
        } else {
            return root;
        }
    }
    return null;
}

public Node<T> findMax(Node<T> tree) {
    if (tree != null) {
        while (tree.getRight()!= null) {
            tree = tree.getRight();
        }
    }
    return tree;
}

public Node<Integer> findMin(Node<Integer> tree) {
    if (tree != null) {
        while (tree.getLeft() != null) {
            tree = tree.getLeft();
        }
    }
    return tree;
}

删除节点

按值删除一个节点，用二分查找递归到需要删除的节点，根据删除节点是否有左右子树分三种情况：

  1. 无左右子树，直接将父节点对其引用置为null。
  2. 只有左子树或者右子树，将父节点对其引用置为其左子树或右子树。
  3. 存在左子树和右子树，在右子树中找最小节点代替被删节点，接着对其右子树的替身节点即最小节点进行删除。
    其中1，2可以合并为一种情况，
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public Node<Integer> delete(Integer t, Node<Integer> root) {
    Node<Integer> temp;
    if (root == null) {
        System.out.println("未找出要删除节点");
    } else if (t < root.getData()) {
        root.setLeft(delete(t, root.getLeft()));
    } else if (t > root.getData()) {
        root.setRight(delete(t, root.getRight()));
    } else { 
        if (root.getLeft()!= null && root.getRight() != null) { // 存在左右子树，找右子树最小节点替换被删节点，对右子树的替身节点删除
            temp = findMin(root.getRight());
            root.setData(temp.getData());
            root.setRight(delete(temp.getData(), root.getRight()));
        } else {
            if (root.getLeft() == null) { // 左子树为空，用右子节点替换本身
                root = root.getRight();
            } else if (root.getRight() == null) { // 右子树为空，用左子节点替换本身
                root = root.getLeft();
            }
        }
    }
    return root;
}

求树高

1
2
3
4
5
6
7
8
9
10
11
12
13
// 6.tree height
// height = max{lh, rh} + 1
public int postOrderGetHeight(Node<T> root) {
    int heightLeft, heightRight, maxHeight;
    if (root != null) {
        heightLeft = postOrderGetHeight(root.getLeft());
        heightRight = postOrderGetHeight(root.getRight());
        maxHeight = heightLeft > heightRight ? heightLeft : heightRight;
        return maxHeight+1;
    } else {
        return 0; // 空树高度
    }
}

附录

Github代码仓库

声明：本站所有文章均为原创或翻译，遵循署名 - 非商业性使用 - 禁止演绎 4.0 国际许可协议，如需转载请确保您对该协议有足够了解，并附上作者名 (Tsukasa) 及原文地址