1.堆中的路径

Problem
将一系列给定数字插入一个初始为空的小顶堆H[]。随后对任意给定的下标i，打印从H[i]到根结点的路径。详细描述

Analysis

  1. 首先建堆有两种方式：(1)元素先用数组按顺序存放好使之满足完全二叉树结构，要构造一个堆，那么我们只需要左右子树为堆，然后调整当前堆为堆即可。(2)首先堆为空，然后按照完全二叉树的结构每次插入一个节点，然后调整当前树为一个堆，即找出插入节点应该在的位置进行插入，与插入排序类似。因为建堆的时间复杂度为O(logN)，有N个元素，时间复杂度为O(NlogN)。根据题目描述只能选择第二种建堆方式。
  2. 建堆过程中可以使用哨兵，如果是最小堆，则H[0]定义为一个足够小的值使得堆元素都大于它。同理可推最大堆应选用一个足够大的值。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include <stdio.h>

#define MINDATA -10001

void printHeap(int numbers[], int index)
{
    int flag = 1;
    while(index >= 2) {
        printf("%d ", numbers[index]);
        index /= 2;
    }
    printf("%d\n", numbers[1]);
}

void insertHeap(int numbers[], int data, int index) 
{
    int i = index;
    for(; numbers[i/2] > data; i /= 2) { // 只要插入元素比父节点i/2小，证明插入元素不再位置i上
        numbers[i] = numbers[i/2];
    }
    numbers[i] = data;
}

int main()
{
    int N, M;
    int index, data;
    #ifndef ONLINE_JUDGE
    freopen("MinHeap.txt", "r", stdin);
    #endif
    
    scanf("%d %d\n", &N, &M);
    int numbers[N+1];
    numbers[0] = MINDATA; // 哨兵 
    for(int i = 1; i <= N; i++) {
        scanf("%d", &data);
        insertHeap(numbers, data, i);
    }
    
    for(int i = 1; i <= M; i++) {
        scanf("%d", &index);
        printHeap(numbers, index);  
    }
    
    return 0;
}

2.File Transfer

Problem
We have a network of computers and a list of bi-directional connections. Each of these connections allows a file transfer from one computer to another. Is it possible to send a file from any computer on the network to any other?详细描述

Analysis

  1. 考察集合的并查集，即查找集合中的元素，求集合并集。
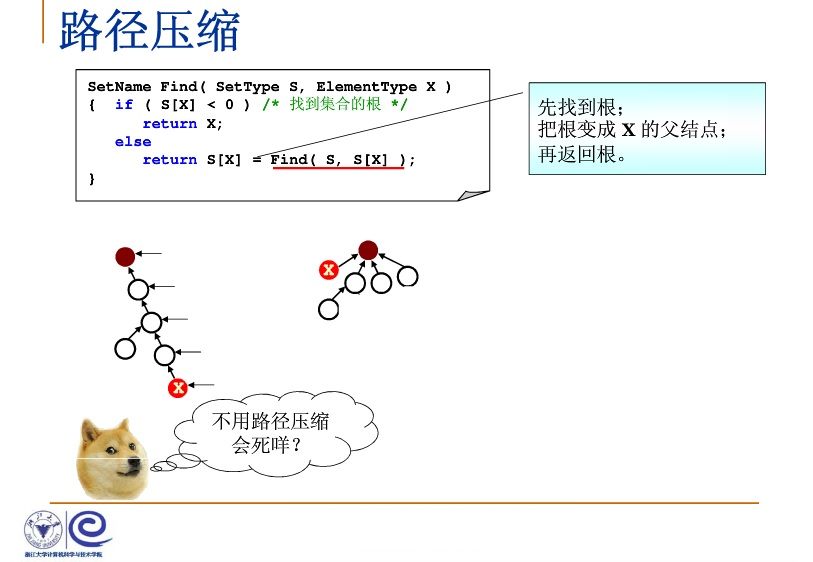
  2. 思路是数组下标i表示各台电脑，s[i]表示电脑的根，如果电脑属于同一个集合那么两台电脑相互连通，根为负数证明该节点是根节点，这里可以利用根节点的根s[root]表示树高的负数或者表示树规模的负数，都称为按秩归并，进行路径压缩可以加快查找效率。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#include <stdio.h>

int count;

void init(int s[], int length) {
    for(int i = 1; i < length; i++) {
        s[i] = -1;
    }
}

int find(int s[], int x) {
    if(s[x] < 0) return x;
    return s[x] = find(s, s[x]); // 不仅将所属树根返回，而且进行了路径压缩 
}

void Union(int x1, int x2, int s[])
{
    int root1 = find(s, x1);
    int root2 = find(s, x2);
    if(root1 != root2) {
        if(s[root2] < s[root1]) { // 如果root2的树高大于root1的树高，矮的root1贴在高的root2上面,即根节点为root2 
            s[root2] += s[root1];
            s[root1] = root2;
            count--;
        } else {
            s[root1] += s[root2];
            s[root2] = root1;
            count--;
        }
    }
}

int main()
{
    int n;
    
    #ifndef ONLINE_JUDGE
    freopen("FileTransfer.txt", "r", stdin);
    #endif
    
    scanf("%d", &n);
    count = n;
    int s[n+1];
    init(s, n+1);
    char ch;
    int x, y;
    scanf("%c", &ch);
    while(ch != 'S') {
        scanf("%d %d", &x, &y);
        if(ch == 'I') {
            Union(x, y, s);
        } else if(ch == 'C') {
            if(find(s, x) == find(s, y)) printf("yes\n");
            else printf("no\n");
        }
        scanf("%c", &ch);
    }
    
    if(count == 1) printf("The network is connected.\n");  
    else printf("There are %d components.\n", count);
    
    return 0;
}

声明：本站所有文章均为原创或翻译，遵循署名 - 非商业性使用 - 禁止演绎 4.0 国际许可协议，如需转载请确保您对该协议有足够了解，并附上作者名 (Tsukasa) 及原文地址