动态规划解决最优化问题

动态规划思想

先来个定位，动态规划大多数应用于求解最优化问题。
故要求问题具有最优子结构性质，通俗来说就是全局最优解包含局部最优解。
动态规划的核心是确定状态和导出状态转移方程。
状态方程的求解多种多样，递归、递推、记忆搜索条条大路通罗马，虽然效率也有差异。

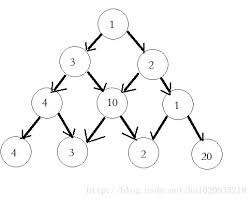
数字三角形问题

1.题目描述：
有一个由非负整数组成的三角形，第n行有n个数，找出一条从三角形的顶到底的路径，使路径经过的数字的和最大。只需计算出和，不需要指明具体路径。如图所示：

2.算法思路：

确定状态：利用二维数组进行坐标定位,把位置(i, j)看作一个状态，定义状态(i, j)的指标函数dp(i, j):从格子(i, j)出发时能得到的最大和(包括格子本身(i, j)的值。
建立状态转移方程：看状态是如何转移的。从(i,j)出发有两种决策，往左下走(i+1,j)对应dp(i+1, j)表示“从(i+1, j)出发后能得到的最大和”、往右下走(i+1, j+1)对应dp(i+1, j+1)，这两个决策自由选择，应选择较大的一个。故得出状态转移方程：

1	dp(i,j) = data(i,j) + max{dp(i+1, j), dp(i+1, j+1)}

3.代码：

import java.util.Scanner;
/**
 * Created by LuoWenqing on 2017/5/10.
 */
public class DigitalTriangle {

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        while (sc.hasNext()) {
            int n = sc.nextInt();
            int[][] data = new int[n][n];
            int[][] dp = new int[n][n];

            for (int i = 0; i < n; i++) {
                for (int j = 0; j <= i; j++) {
                    data[i][j] = sc.nextInt();
                    dp[i][j] = -1;
                }
            }
            System.out.println(solve(0, 0, dp, data));
            //System.out.println(solve2(0, 0, data));
            //System.out.println(solve3(dp, data));
        }
    }

    // 递归
    public static int solve2(int i, int j, int[][] data) {
        // 递归方式，重叠子问题，重复计算，效率低
        if (i == data.length - 1) return data[i][j];
        return data[i][j] + Math.max(solve2(i+1, j, data), solve2(i+1, j+1, data));
    }

    // 递推
    public static int solve3(int[][] dp, int[][] data) {
        for (int j = 0, endPos = dp.length - 1; j <= endPos; j++) {
            dp[endPos][j] = data[endPos][j];
        }

        for (int i = dp.length - 2; i >= 0; i--) {
            for (int j = 0; j <= i; j++) {
                dp[i][j] = data[i][j] + Math.max(dp[i+1][j], dp[i+1][j+1]);
            }
        }
        return dp[0][0];
    }

    // 记忆搜索
    public static int solve(int i, int j, int[][] dp, int[][] data) {
        // 判断是否被计算过
        if (dp[i][j] >= 0) return dp[i][j];
        // 如果是最后一行，直接返回data[i][j]
        if (i == dp.length - 1) return data[i][j];
        // 否则，递归执行状态方程，d[i][j]设置从(i,j)出发后能得到最大和
        dp[i][j] = data[i][j] + Math.max(solve(i+1, j, dp, data), solve(i+1, j+1, dp, data));
        return dp[i][j];
    }
}

币值最大化问题

1.题目描述：
给定一排n个硬币，其面值均为正整数c1，c2，...，cn，这些整数并不一定两两不同。请问如何选择硬币，使得在其原始位置互不相邻的条件下，所选硬币的总金额最大。

2.算法思路：

确定状态：dp(i)表示前i个硬币中能选到的最大币值.
状态转移方程：n个硬币中，分两种情况：选最后一枚硬币(coin(n)+dp(n-2))，不选最后一枚硬币dp(n-1)，我们选择两者中取到硬币总值最大的，综上，得到状态方程：

1 2	dp(n) = max{coin(n) + dp(n - 2), dp(n - 1)}, n>1 dp(0) = 0, dp(1) = coin(1)

也可以根据递归、递推、记忆搜索策略写出代码。

3.代码：

import java.io.BufferedInputStream;
import java.io.FileInputStream;
import java.io.InputStream;
import java.util.Scanner;

/**
 * Created by LuoWenqing on 2017/5/10.
 */
public class CoinRow {

    // 递归
    public static int maxCoinVal(int[] data, int n) {
        if (n == 0 || n == 1) return data[n];
        return Math.max(data[n] + maxCoinVal(data, n - 2), maxCoinVal(data, n - 1));
    }

    // 递推
    public static int maxCoinVal2(int[] coin) {
        int[] dp = new int[coin.length];
        dp[0] = 0;
        dp[1] = coin[1];
        for (int i = 2; i < coin.length; i++) {
            dp[i] = Math.max(coin[i] + dp[i - 2], dp[i - 1]);
        }
        return dp[coin.length - 1];
    }

    public static void main(String[] args) throws Exception{
        InputStream is = new BufferedInputStream(new FileInputStream("coinrow.txt"));
        System.setIn(is);

        Scanner sc = new Scanner(System.in);
        while (sc.hasNext()) {
            int n = sc.nextInt();
            int[] coin = new int[n + 1];
            coin[0] = 0;
            for (int i = 1; i <= n; i++) {
                coin[i] = sc.nextInt();
            }

            System.out.println(maxCoinVal(coin, n));
            System.out.println(maxCoinVal2(coin));
        }
    }
}

找零问题

1.题目描述：
需找零金额为n，现有面值为d1<d2<...<dm的硬币，数目没有限制，最少要用多少张硬币？

2.算法思路：

状态：输入有总金额n，面值硬币序列coin[]。设dp(n)为总金额为n时需要数量最少的硬币数目。
方程：

1
2
3

当n > 0 且 n >= coin[j], dp(n) = min{dp(n - coin[j])} + 1

n = 0, dp(0) = 0

3.代码：

import java.io.*;
import java.util.Scanner;

/**
 * Created by LuoWenqing on 2017/5/10.
 */
public class MinNumCoin {
    
    public static int minNum(int[] coin, int n) {
        int[] dp = new int[n+1];
        dp[0] = 0;
        for (int i = 1; i <= n; i++) {
            int temp = coin[coin.length - 1] + 1;
            for (int j = 1; j < coin.length && i >= coin[j]; j++) {
                temp = Math.min(dp[i - coin[j]], temp);
            }
            dp[i] = temp + 1;
        }
        return dp[n];
    }

    public static void main(String[] args) throws FileNotFoundException {
        InputStream is = new BufferedInputStream(new FileInputStream("minnumcoin.txt"));
        System.setIn(is);

        Scanner sc = new Scanner(System.in);
        while (sc.hasNext()) {
            int n = sc.nextInt();
            int m = sc.nextInt();
            int[] coin = new int[m + 1];
            coin[0] = 0;
            for (int i = 1; i <= m; i++) {
                coin[i] = sc.nextInt();
            }
            System.out.println(minNum(coin, n));
        }
    }
}

连续子序列最大和

1.题目描述：
给定K个整数的序列{ N1, N2, ..., NK }，其任意连续子序列可表示为{ Ni, Ni+1, ..., Nj }，其中 1 <= i <= j <= K。最大连续子序列是所有连续子序中元素和最大的一个，例如给定序列{ -2, 11, -4, 13, -5, -2 }，其最大连续子序列为{ 11, -4, 13 }，最大和为20。

2.算法思路：
学了动态规划，也要知道这道题非动态规划的思路还是很简单的，暴力求解：从0-(n-1)的某个位置开始的子序列最大和，一直加到最后，sum(current...x) > max比较，总是保存最大的一个。为了降低点复杂度，动态规划O(n)大法吧：

状态；设有数字序列numbers[0...n-1],选择连续子序列最大和，注意从和最大的角度考虑，maxSum(i)表示以numbers[i]结尾的序列的最大和。那么以当前元素numbers[i]结尾可以划分为两种情况：加上前面的maxSum(i-1), 不加上前面的maxSum(i-1)。为什么呢，可以这么想，如果前面以numbers[i-1]为尾节的子序列即maxSum(i-1)为负则不加，为正当然是要加上啦。
方程：

1	maxSum(i) = max{numbers[i] + maxSum(i-1), numbers[i]}

3.代码

import java.io.*;
import java.util.Arrays;
import java.util.Scanner;

/**
 * Created by LuoWenqing on 2017/5/10.
 */
public class SequenceMax {
    public static void main(String[] args) throws FileNotFoundException {
        InputStream is = new BufferedInputStream(new FileInputStream("maxseq.txt"));
        System.setIn(is);
        Scanner sc = new Scanner(System.in);
        while(sc.hasNext()) {
            int n = sc.nextInt();
            int[] numbers = new int[n+1];
            numbers[0] = 0;

            int[] maxSum = new int[n+1];
            maxSum[0] = -1;

            for (int i = 1; i <= n; i++) {
                numbers[i] = sc.nextInt();
                maxSum[i] = -1;
            }
            initDp(numbers, maxSum, n);
            Arrays.sort(maxSum);
            System.out.println(maxSum[n]);

            System.out.println(maxSeqSum(numbers, maxSum));
            System.out.println(maxSeqSum2(numbers));
        }
    }

    // 记忆搜索，对于序列numbers, 求出以numbers[tailPos]的连续子序列最大和，用maxSum[tailPos]保存
    public static int initDp(int[] numbers, int[] maxSum, int tailPos) {
        if (tailPos == 0) {
            return 0;
        }
        if (maxSum[tailPos] >= 0) {
            return maxSum[tailPos];
        }
        return maxSum[tailPos] = Math.max(numbers[tailPos] + initDp(numbers, maxSum, tailPos - 1), numbers[tailPos]);
    }

    // 递推
    public static int maxSeqSum(int[] numbers, int[] maxSum) {
        for (int i = 1, end = numbers.length - 1; i <= end; i++) {
            maxSum[i] = Math.max(numbers[i] + maxSum[i-1], numbers[i]);
        }
        Arrays.sort(maxSum);
        return maxSum[maxSum.length - 1];
    }

    // 优化递推
    public static int maxSeqSum2(int[] numbers) {

        int maxSum, maxHere;
        maxSum = maxHere = numbers[0];

        for (int i = 1, end = numbers.length - 1; i <= end; i++) {
            if (maxHere <= 0) {
                maxHere = numbers[i];
            } else {
                maxHere += numbers[i];
            }
            // 如果maxHere大于0，则更新
            if (maxHere > maxSum) {
                maxSum = maxHere;
            }
        }
        return maxSum;
    }
}

0/1背包问题

1.题目描述：
有 n 种物品，物品 i 的体积为 v[i], 价值为 p[i]. 假定所有物品的体积和价格都大于 0, 以及背包的体积为 V.
问：选择哪些物品可使在体积不超过 V 的情况下使物品的总价值最大，并求出这个总价值，且每种物品只能选择 0 个或 1 个

2.算法思路：

状态分析：考虑由前i个物品，当前背包的体积为j，dp(i, j)为给定的前i件物品中，体积为j的背包能放进的最大价值。
导出状态转移方程：递推思想，如果体积j > volume[i],那么dp(i, j)有两种策略：包括第i件物品最大价值为dp(i-1, j-volume[i]) + values[i]，不包括第i件物品最大价值为dp(i-1,j)，取最大者。

1
2
3

dp(i, j) = max{dp(i-1, j), dp(i-1, j-volume[i]) + values[i]}, j > volume[i]
dp(i, j) = dp(i-1, j), j < volume[i]    
初始化条件：j >= 0时，dp(0, j) = 0; i >= 0时，dp(i, 0) = 0;

3.代码：

import java.io.*;
import java.util.Arrays;
import java.util.Scanner;

/**
 * Created by LuoWenqing on 2017/5/11.
 */
public class Knapsack {

    public static void main(String[] args) throws FileNotFoundException {
        InputStream is = new BufferedInputStream(new FileInputStream("knapsack.txt"));
        System.setIn(is);
        Scanner sc = new Scanner(System.in);
        while (sc.hasNext()) {
            int V = sc.nextInt(); // 背包的体积

            int n = sc.nextInt();   // 物品的数量
            int[] values = new int[n+1]; // 物品的价值
            values[0] = 0;
            int[] volume = new int[n+1]; // 物品的体积
            volume[0] = 0;

            for (int i = 1; i <= n; i++) {
                values[i] = sc.nextInt();
                volume[i] = sc.nextInt();
            }
            System.out.println(maxValue(values, volume, V));

            int[][] dp = new int[values.length][V+1];
            for (int i = 0; i < values.length; i++) {
                Arrays.fill(dp[i], 0);
            }
            System.out.println(maxValue2(values, volume, dp, values.length - 1, V));
        }
    }

    // 递推
    public static int maxValue(int[] values, int[] volume, int V) {
        // 二维维护表
        int[][] dp = new int[values.length][V + 1];
        // 初始条件，虽然java默认初值为0
        for (int j = 0; j <= V; j++) {
            dp[0][j] = 0;
        }
        for (int i = 0; i < values.length; i++) {
            dp[i][0] = 0;
        }

        for (int i = 1; i < values.length; i++) {
            for (int j = 1; j <= V; j++) {
                if (j < volume[i]) {
                    dp[i][j] = dp[i - 1][j]; // 不能装入背包
                } else {
                    if (dp[i - 1][j - volume[i]] + values[i] > dp[i - 1][j]) { // 选择价值较大者
                        dp[i][j] = dp[i - 1][j - volume[i]] + values[i]; // 包括第i件物品
                    } else {
                        dp[i][j] = dp[i - 1][j]; // 不包括第i件物品
                    }
                }
            }
        }
        return dp[values.length - 1][V];
    }

    // 记忆搜索
    public static int maxValue2(int[] values, int[] volume, int[][] dp, int i, int j) {
        if (i == 0 || j == 0) {
            return 0;
        }
        if (dp[i][j] > 0) {
            return dp[i][j];
        }
        if (j < volume[i]) {
            return dp[i][j] = maxValue2(values, volume, dp, i-1, j);
        }
        return dp[i][j] = Math.max(maxValue2(values, volume, dp, i - 1, j - volume[i]) + values[i], maxValue2(values, volume, dp, i-1, j));
    }
}

声明：本站所有文章均为原创或翻译，遵循署名 - 非商业性使用 - 禁止演绎 4.0 国际许可协议，如需转载请确保您对该协议有足够了解，并附上作者名 (Tsukasa) 及原文地址

Tsukasa の部屋

动态规划解决最优化问题

动态规划思想

数字三角形问题

币值最大化问题

找零问题

连续子序列最大和

0/1背包问题

Tsukasa

「My Homepage」
「About Me」
「My Links」

Web Developer

Shenzhen

动态规划解决最优化问题

动态规划思想

数字三角形问题

币值最大化问题

找零问题

连续子序列最大和

0/1背包问题

Tsukasa

「My Homepage」「About Me」「My Links」

Web Developer

Shenzhen

「My Homepage」
「About Me」
「My Links」