这篇文章记录了五篇算法练习题,内容如下:
- 求二叉树到所有叶子节点的路径和
- 正则表达式‘.’和‘*’匹配
- 用两个栈实现队列
- 链表反转
- 合并两个排序链表
求二叉树到所有叶子节点的路径和
阿里2017实习招聘在线编程题:
对于一个由一位十进制整数构成的二叉树,如果深度不超过4,可以用一个三位十进制整数构成的数组表示,具体规则如下:
1.百位树表示树的层次L,1<=L<=4;十位数表示在该层次中的位置P,1<=P<=8;个位树表示数值V。
2.数组里,L一定是单增的,也就是说后一个树的L大于等于前一个树的L。
3.对于同一个L,P也是单增的,也就是说在L不变的情况下,后一个数的P大于等于前一个数的P。
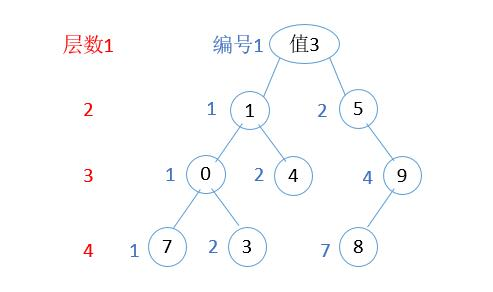
例如:[113, 215, 221]对应的数是:
3
/ \
5 1
现在要求这个树所有到叶子节点的路径和,对于[113, 215, 221]这棵树,有两个路径3-5和3-1,路径和是(3+5)+(3+1)= 12
解题思路:
- L,P,V三个输入参数,该二叉树最多为2L-1个节点,故可用二维数组
array[L][P] = V的结构描述,这里扩大数组为array[6][17]是为了统一处理。
- L决定层数,P决定在该层中的位置,V表示节点的值,举例下图。设位置无树节点时,值为-1,先全部初始化。
- 从根节点向下扫描,当前节点存在,判断其子节点是否存在,如果都不存在,证明当前结点为叶子节点,利用完全二叉树性质求出该节点的父节点,累加节点值V求出该路径长度;否则继续搜索。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
| import java.util.Scanner;
public class BPath {
public static void main(String[] args) {
int L;
int P;
int V;
int sum = 0;
int[][] arr = new int[6][17];
for (int i = 0; i < 6; i++) {
for (int j = 0; j < 17; j++) {
arr[i][j] = -1;
}
}
Scanner scanner = new Scanner(System.in);
int number = scanner.nextInt();
while (number != 0) {
L = number/100;
P = number/10%10;
V = number%10;
arr[L][P] = V;
number = scanner.nextInt();
}
System.out.println("矩阵表示:");
for (int i = 1; i <= 4; i++) {
for (int j = 1; j <= 8; j++) {
System.out.print(arr[i][j]+" ");
if (arr[i][j] != -1 && (arr[i+1][j*2] == -1 && arr[i+1][j*2-1] == -1)) {
for (int x = i, y = j; x >= 1; x--) {
sum += arr[x][y];
if (y >= 1 && y % 2 == 1) {
y = y / 2 +1;
} else if (y >= 1 && y % 2 == 0){
y = y/2;
}
}
}
}
System.out.println();
}
System.out.println("路径和为:" + sum);
}
}
|
请实现一个函数用来匹配包括.和*的正则表达式。模式中的字符.表示任意一个字符,而*表示它前面的字符可以出现任意次(包含0次)。 在本题中,匹配是指字符串的所有字符匹配整个模式。例如,字符串aaa与模式a.a和ab*ac*a匹配,但是与aa.a和ab*a均不匹配。
思路:递归策略,匹配分三种情况:
- 匹配成功:串和模式都到达末尾,返回true
- 匹配失败:模式先到达末尾,返回false
- 当前字符匹配:字符串和模式当前字符匹配(字符一模一样或者模式当前位为
.),则按照下一个字符是否为.;,是则根据匹配0次,1次,多次三种情况,设置字符串和模式移动相应的位置,返回三种情况匹配的并集(||);下一个字符不为.;,则返回模式与串后移一位的匹配结果。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
| public class Solution {
public boolean match(char[] str, char[] pattern) {
if (str == null || pattern == null) {
return false;
}
int strIndex = 0;
int patternIndex = 0;
return matchCore(str, strIndex, pattern, patternIndex);
}
public boolean matchCore(char[] str, int strIndex, char[] pattern, int patternIndex) {
if (strIndex == str.length && patternIndex == pattern.length) {
return true;
}
if (strIndex != str.length && patternIndex == pattern.length) {
return false;
}
if (patternIndex + 1 < pattern.length && pattern[patternIndex+1] == '*') {
if ((strIndex != str.length && pattern[patternIndex] == str[strIndex])
|| (pattern[patternIndex] == '.' && strIndex != str.length)) {
return matchCore(str, strIndex, pattern, patternIndex + 2)
|| matchCore(str, strIndex + 1, pattern, patternIndex + 1)
|| matchCore(str, strIndex + 1, pattern, patternIndex);
}
return matchCore(str, strIndex, pattern, patternIndex + 2);
}
if ((strIndex != str.length && str[strIndex] == pattern[patternIndex])
|| (pattern[patternIndex] == '.' && strIndex != str.length)) {
return matchCore(str, strIndex + 1, pattern, patternIndex + 1);
}
return false;
}
}
|
用两个栈实现队列
用两个栈来实现一个队列,完成队列的Push和Pop操作。 队列中的元素为int类型。
思路:
- 栈1进栈的顺序即元素入队顺序,出栈到栈2中后,栈2元素出栈的顺序就变成了出队的元素。
- 因此每次出队时,判断栈2是否为空,不为空直接出栈,为空则先从栈1的队列转移到栈2中,然后栈2出栈的顺序才是原来队列先进先出的顺序。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| import java.util.Stack;
public class StackChangeToQueue {
Stack<Integer> stack1 = new Stack<>();
Stack<Integer> stack2 = new Stack<>();
public void push(int node) {
stack1.push(node);
}
public int pop(){
if (stack2.empty() && stack1.empty()) {
throw new RuntimeException("Queue is empty!");
}
if (stack2.empty()) {
while (!stack1.empty()) {
stack2.push(stack1.pop());
}
}
return stack2.pop();
}
}
|
链表反转
输入一个链表,反转链表后,输出链表的所有元素。
解题思路:
- 考虑一般情况,分为已经反转好的部分A,等待反转的部分B。反转的操作是,将B中的节点逐一指向反转好的部分的节点。比如原来是
1->2->3->4->5->6变成1<-2<-3 4->5->6后,下一步是1<-2<-3<-4 5->6
- 那么为了实现链表的反转,我们需要记录当前节点head,当前节点的前驱pre(已经反转好的链表的头),当前结点的后继next(如果不保存该节点,
head.next = pre后就找不到待反转的部分了),执行下面的四个操作:
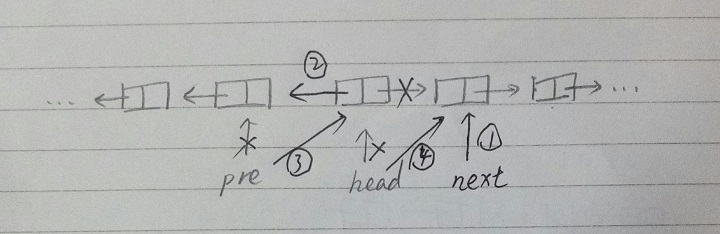
1
2
3
4
| next = head.next;
head.next = pre;
pre = head;
head = next;
|
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| class ListNode {
int val;
ListNode next = null;
ListNode(int val) {
this.val = val;
}
}
public class ReverseLinkedList {
public ListNode ReverseList(ListNode head) {
if (head == null) {
return head;
}
ListNode pre = null;
ListNode next = null;
while (head != null) {
next = head.next;
head.next = pre;
pre = head;
head = next;
}
return pre;
}
}
|
合并两个排序链表
输入两个单调递增的链表,输出两个链表合成后的链表,当然我们需要合成后的链表满足单调不减规则。
思路:
- 看到该题时,我首先想到的是归并排序算法的归并过程。考虑一般情况,当两个链表都不为空,比较两个链表的元素,值小的元素作为第三条链表的下一个元素,分别后移位置循环比较。
- 特殊情况是,链表list1或list2为空,直接返回另一条链表即可。
非递归实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
| class ListNode {
int val;
ListNode next = null;
ListNode(int val) {
this.val = val;
}
}
public class Solution {
public ListNode Merge(ListNode list1, ListNode list2) {
if (list1 == null) {
return list2;
}
if (list2 == null) {
return list1;
}
ListNode mergeHead = new ListNode(0);
ListNode current = mergeHead;
while (list1 != null || list2 != null) {
if (list1.val < list2.val) {
current.next = list1;
current = list1;
list1 = list1.next;
} else {
current.next = list2;
current = list2;
list2 = list2.next;
}
}
if (list1 != null) {
current.next = list1;
}
if (list2 != null) {
current.next = list2;
}
mergeHead = mergeHead.next;
return mergeHead;
}
}
|
递归实现
其实我一直在思考,什么样的情况可以转化为或者说运用递归算法。其实可以这么考虑,如果要解决这个问题,我能否构造一个递推公式?又或者说问题变小后是否具有同样的特征。比如这里的两个链表的合并,如果我能分为连接好的部分,只需将剩下两条链表连接,而这两条链表的连接与父问题又具有同样的解法,如此,可以得到代码简洁的递归算法。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| public class Solution {
public ListNode Merge(ListNode list1, ListNode list2) {
if (list1 == null) {
return list2;
}
if (list2 == null) {
return list1;
}
if(list1.val < list2.val) {
list1.next = Merge(list1.next, list2);
return list1;
} else {
list2.next = Merge(list1, list2.next);
return list2;
}
}
}
|
声明:本站所有文章均为原创或翻译,遵循署名 - 非商业性使用 - 禁止演绎 4.0 国际许可协议,如需转载请确保您对该协议有足够了解,并附上作者名 (Tsukasa) 及原文地址



