前言
线性表是数据结构中最基础的结构,本文从最简单的线性表开始,带你领略数据结构的魅力(手动滑稽),主要内容有:
- 线性表的基本概念
- 顺序存储与链式存储
- 顺序表与单链表比较
TABLE OF CONTENTS
线性表的定义
线性表(List):由零个或多个数据元素组成的有限序列,像是这样的:
A1 —> A2 —> … —> Ai-1 —> Ai —> Ai+1 —> … —> An
其中,Ai-1称为Ai直接前驱,Ai+1成为Ai的直接后继。首元素A1无直接前驱,尾元素An无直接后继,中间元素都有唯一直接前驱、直接后继。n=0时,为空表;n>=0,为非空线性表。一个数据元素可以由若干个数据项组成。
抽象表示
1 | ADT LinearList |
学习线性表,关键掌握如何对线性表进行下列操作:
- 初始化,判表是否为空,求表长;
- 插入,删除,访问节点。
顺序存储与链式存储
按存储结构划分为顺序表,链表。
顺序存储结构,指在内存中用地址连续的一块存储空间依次存放线性表中的各元素。
链式存储结构,用一组任意的存储单元存储线性表的数据元素,这组存储单元可以是连续的,也可以是不连续的。
换句话说,顺序表逻辑、物理相邻;链表逻辑相邻,物理不要求相邻。
顺序表
线性表的顺序存储结构,指在内存中用地址连续的一块存储空间依次存放线性表中的各元素。
1 | class SeqList { |
描述顺序存储结构需要三个属性(数据域部分)
- 动态数组element, 各个元素构成的集合
- 表最大存储容量MaxSize
- 表当前长度length,即当前有意义的元素个数
我喜欢用图描述顺序表:
顺序表中各个元素的所占存储空间是连续的,如下图所示,如果进行插入节点(第二行)、删除节点(第三行),需要对表尾的所有元素整体进行移动,可以理解为我们体育课排队时中间插入了一个人,或者走掉一个人的情况。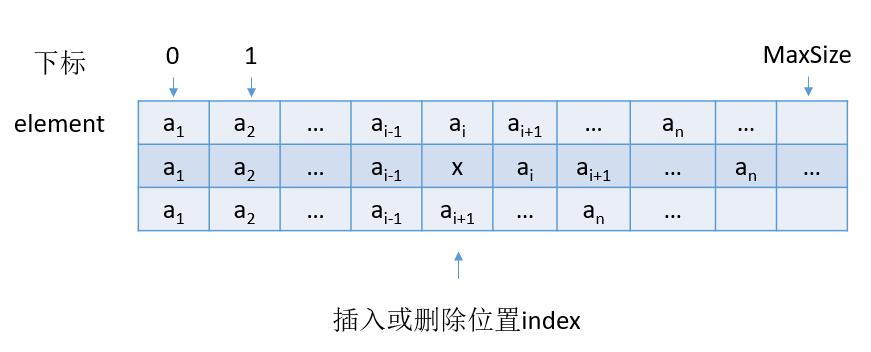
初始化
1 | void InitList(int MaxSize) { |
访问节点
访问包括按值访问、按下标索引节点两种。实现起来也很简单,只需循环遍历,按照条件定位节点。
1 | /* 给定元素e,返回该元素位置 */ |
插入节点
算法步骤:
- 特殊情况处理,比如越界,表满
- 先将插入位置及其后面的元素整体后移
- 赋值,长度加一
1 | bool ListInsert(int index, T &e) { |
删除节点
算法步骤:
- 特殊情况处理,如越界,为空
- 删除节点后面的元素整体向前移动
- 长度减一
1 | bool ListDelete(int index, T &e) { |
链表
线性表的链式存储结构,用一组任意的存储单元存数据元素,这组存储单元可以是连续的,也可以是不连续的。如下图所示:
链表是一种灵活神奇的数据结构。定义一个单链表通常使用两个类,即节点类ListNode和链表类LinkedList,如何表达两者关系呢?可以选择复合类、内部类的方式,下面基于复合类方式说明。
其中,ListNode类包含数据域和指针域。数据域可以由基本数据类型组成,也可以是类类型等,指针域用于存放下一个节点的地址。ListNode类关心的是对节点本身的管理,如setter、getter等。LinkedList类包含ListNode属性,两者是聚合关系,关心对整条链的操作,如查找,插入、删除节点等。
1 | class ListNode// 节点类ListNode |
创建链表
创建链表有头插,尾插两种策略。差别看图:
头插法:
1 | while(输入不为结束条件) { |
尾插法:
1 | while(输入不为结束条件) { |
如果链表为空需要特殊处理,使用头节点代替头指针,则链表的元素都可以看作表中间的元素,故而可以一视同仁,统一链表的查找,插入,删除等操作。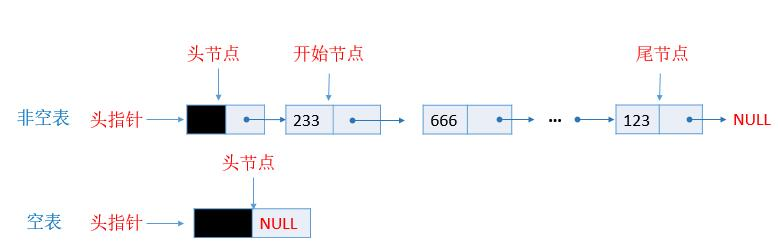
头指针与头结点的区别:
| 头指针 | 头结点 |
|---|---|
| 头指针即链表指向第一个结点的指针,若链表有头结点,则是指向头结点的指针 | 头结点是为了操作的统一和方便而设立的,放在第一元素的结点之前,其数据一般无意义(也可能存放链表的长度) |
| 头指针具有标识作用,所以常用头指针冠以链表的名字 | 有了头结点,对在第一元素结点前插入结点和删除第一节点,其操作与其它结点的操作就统一了 |
| 无论链表是否为空,头指针均不为空,头指针是链表的必要元素 | 头结点不一定是链表的必要元素 |
插入节点
插入节点可以分为前插法,后插法。后插策略如图所示: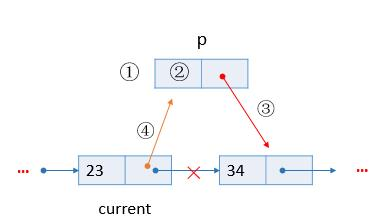
算法步骤:
- 创建新节点p
- 数据域赋值
- 当前节点current的后继作为新节点的后继
- 新节点p作为当前节点current的后继
代码:
1 | p->next = current->next; |
前插法类似,只是按照插入条件(位置或按值)定位插入位置前一个节点,这里涉及到current和current->next的妙用了,请看:
1 | while (current && current->data != e) { //...} |
前者关注当前节点,后者关注前驱节点。这个例子前插可以通过先做后插,再通过数据交换实现在节点后面插入的效果,后插也可以通过前插进行转换。链表是一个很灵活的结构,删除节点同样可以利用这个小技巧
删除节点
删除节点也有删除当前节点、删除后继节点两种,同时也可以运用替身法实现两者的转化。下面给出删除当前节点的两种实现方式:
借助前驱节点,即借用prev保存当前结点current的前驱。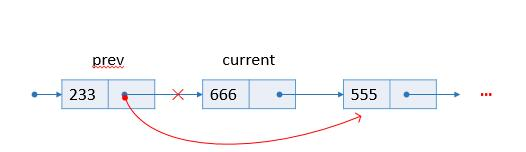
1 | prev->next = current->next; |
替身法
1 | pnext = current->next; |
链表的分类
按实现角度分:静态链表、动态链表。对于没有指针的语言,可以用数组描述链表,称为静态链表;而用指针进行动态分配回收内存空间的,称为动态链表。
静态链表:类比上面介绍的动态单链表,数组的元素设置两个数据域: data和cur。数据域data,用来存放数据元素,也就是通常我们要处理的数据;而cur相当于单链表中的next指针,存放该元素的后继,即下一个节点数组元素的下标,cur称为游标。 因为静态链表的空间是实现分配好的,所以,我们需要自定义内存的申请和释放,而我们可以将所有未被使用过的及已被删除的分量用游标链成一个备用的链表,每当进行插入时,便可以从备用链表上取得第一个结点作为待插入的新结点。
按链接方式分:单链表、循环链表、双向链表。
循环链表:将单链表中尾节点的指针域由NULL改为指向头节点,使单链表连接成一个环,首尾相接的链表称循环链表。循环链表实现了从一个节点出发,访问整条链表的每个节点。下面是非空的循环链表示意图:
由于存在头节点,单向循环链表存在尾指针rear条件下访问开始节点即rear->next->next,只需O(1)的时间复杂度。
双向链表:单链表的每个节点中,增加一个指向前驱的指针域。下面简单描述双向链表的插入节点、删除节点操作。
插入节点: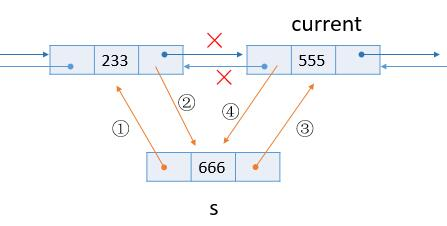
1 | s->prior = current->prior; |
删除节点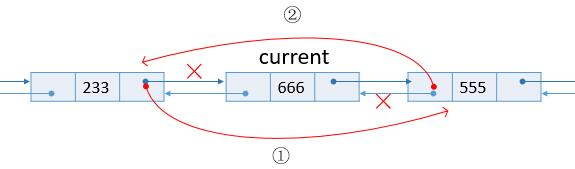
1 | current->prior->next = current->next; |
顺序表与单链表比较
顺序表与单链表的选取可以考虑存储方式、时间性能、空间性能方面的要求。
- 顺序表需预先分配内存空间,存储规模固定,分配少了易发生溢出;单链表按需分配存储空间,元素个数不受限制
- 顺序表查找时间复杂度为
O(1),插入和删除为O(n);单链表查找为O(n),插入和删除为O(n)
因此,存储空间无特别要求时,需要频繁进行查找访问操作时,选用顺序存储;频繁进行插入删除操作时,选用链式结构。
总结
至此,把一直想总结的线性表知识写完了。写博客是一个知识整理的过程,你会去查阅许多知识,学习许多知识,把自己之前忽略的、认为重要的知识点进行归纳,万一自己忘了在翻来看看温故而知新,虽然不排除我靠,我怎么写出这样的渣文来的羞耻不已罢了。
声明:本站所有文章均为原创或翻译,遵循署名 - 非商业性使用 - 禁止演绎 4.0 国际许可协议,如需转载请确保您对该协议有足够了解,并附上作者名 (Tsukasa) 及原文地址

